Evaluación del algoritmo

En esta sección se observa el resultado de las distintas evaluaciones al algoritmo MSSR.

Visualizaciones según tratamiento temporal del stack de imágenes

Distintos tratamientos temporales producen diferentes imágenes. Cada uno tiene sus ventajas y desventajas. Usar la mediana tiene la ventaja de eliminar los outliers pero puede ser que no estemos capturando el fenómeno en su totalidad ya que nada garantiza que se capture el fenómeno completo. Si el fenómeno parpadea muy rápidamente posiblemente sea mejor utilizar la varianza ya que alcanzaremos a capturar más de él pero si es una imagen continua se podria perder información. La opción de usar la media tiene en cuenta los outliers y podría producir resultados no esperados. A continuación se muestran resultados de aplicar el algoritmo con Ampliación=5 , hs=3 y Orden=1.

Figura 1: Resultado para distintos procesamiento temporal

Diferencias en la visualización de distintos parámetros

Dejando fijos la ampliación en 5 y el hs en 3 nos disponemos a ver el efecto de la variación del orden en nuestro algoritmo. Se puede ver cómo a medida que se incrementa el orden la imagen tiende a mantener el valor del punto más brillante mientras mantiene el resto de la estructura cada vez más apagada pero nunca difuminandóse. En esta sección se emplea un procesamiento temporal de media a todas las imágenes.

Figura 2: MSSR con Ampliación=5 , hs=3 y variación de Orden

Dejando fijo el orden en 0 y el hs en 3 procedemos a variar la ampliación. Aqui se puede apreciar como si bien el zoom es digital y un producto matemático nos permite tener más resolución siendo tratado por el algoritmo.

Figura 3: MSSR con Orden=0, hs=3 y variación de ampliación

Por ultimo dejamos fijos el orden en 0 y la ampliación en 5 y procedemos a variar el hs. En esta imagen es donde se ven menos cambios lo cual es coherente ya que el principal propósito de la variación del ancho del kernel es determinar que solo le estemos aplicando el algoritmo a una sola estructura de interés que es el caso para todas las imágenes de prueba.

Figura 4: MSSR con Orden=0, Ampliación=5 y variación de hs

Tiempos de ejecución

Debido a ser un algoritmo robusto que puede ser usado con una infinidad de parámetros parece ser de vital importancia el tiempo de ejecución. Es por esto que se decide ahondar en cómo evolucionan a medida que varían los parámetros. Los parámetros base con los que se calculó el algoritmo son Orden=0, Ampliación=5, hs=3 y un procesamiento temporal de media, variándose cada uno para ver su evolución a través del tiempo.

El tamaño de la imagen parece hacer escalar al tiempo de manera cuadrática.

Figura 5: Tiempo en función de tamaño de la imagen

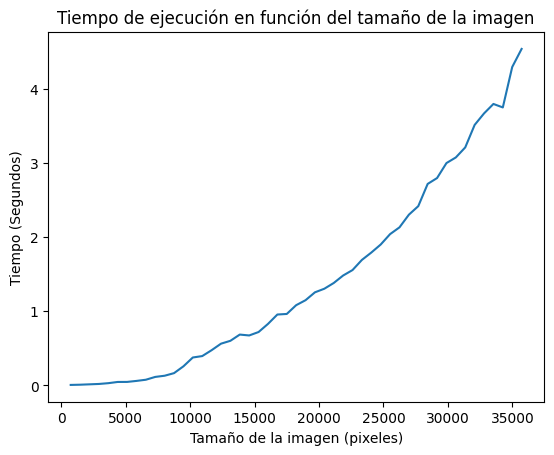
El tamaño del kernel parece hacer escalar al tiempo de manera cuadrática.

Figura 6: Tiempo en función de tamaño del kernel

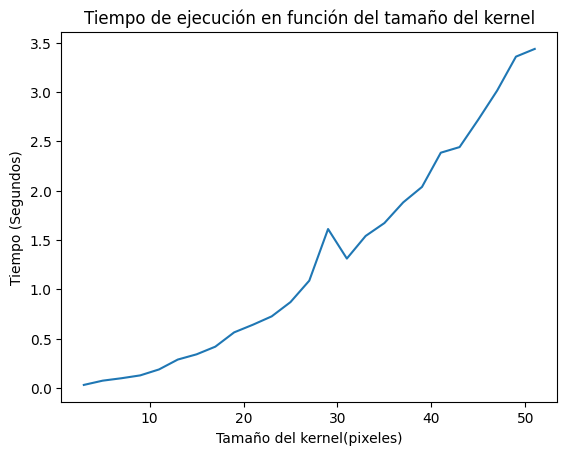
El orden parece no tener una relacion cuadratica con el tiempo. También es importante notar cómo incrementar el orden solo implica enlentecer operaciones aritmeticas sobre la imagen debidoa que ya fue calculada la media desplazada por lo que los tiempos de procesamiento parecen ser mucho menores.

Figura 7: Tiempo en función de tamaño de la imagen

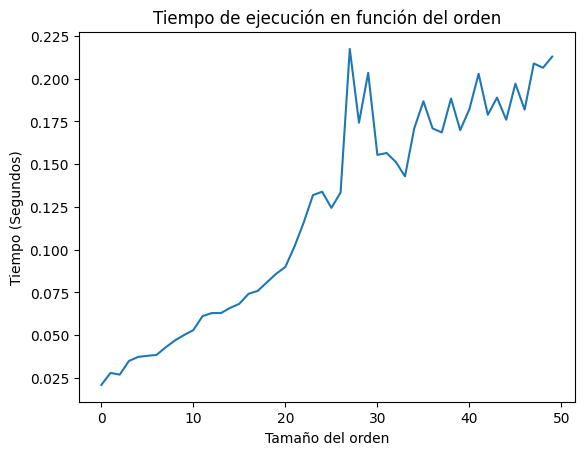
Importancia del kernel espacial

En el cálculo de la media desplazada se emplea una ponderación gaussiana con respecto al punto central. Se trata de una operación que puede llegar a ser computacionalmente costosa asi que se decidió fijarse los efectos que tiene en tiempos de ejecución y en resultados. Para esto se removió el código del algoritmo resultando de la siguiente manera:

Implementación en python

def sfMSSRSNOESPACIAL(img,ampliacion,hs,order,temporal=None):



    #Procesamiento temporal
    if temporal=='mean':
        img = np.mean(img,axis=0)
    elif temporal == 'var':
        img = np.var(img,axis=0)

    #Ampliamos la imagen con un factor de ampliación e interpolacion bicubica
    img = zoom(img, ampliacion, order=3)
    width , height = img.shape
    #Padeamos la imagen para poder recorrerla
    Ipad=np.pad(img,hs,'symmetric')
    #Guardamos la diferencia máxima entre el punto y el ancho de banda para normalizar
    M=np.zeros((width,height))
    for i in range(-hs,hs+1):
        for j in range(-hs,hs+1):
            if i!=0 and j!=0:
                HS=Ipad[hs+i:width+hs+i,hs+j:height+hs+j]
                M=np.maximum(M,np.abs(img-HS))

    PesosAcum=np.zeros((width,height))
    ValoresAcum=np.zeros((width,height))

    #Recorremos el filtro con la imagen(Es una optimización necesaria para no recorrer la imagen)
    for i in range(-hs,hs+1):
        for j in range(-hs,hs+1):
            if i!=0 and j!=0:
                HS=Ipad[hs+i:width+hs+i,hs+j:height+hs+j]
                kernelIntensidad=np.exp(-pow((img-HS)/M,2))

                Pesos=kernelIntensidad
                PesosAcum=PesosAcum+Pesos
                ValoresAcum=ValoresAcum+Pesos*HS

    MS=img-(ValoresAcum/PesosAcum)
    MS[MS<0]=0
    MS[np.isnan(MS)]=0

    I0=MS/max(map(max,MS))
    I3=I0
    x3= img/max(map(max,img))

    for i in range(order):
        #Calculamos la diferencia entre la original y la imagen MS ambas normalizadas
        I4 = x3 - I3
        #Calculamos el complemento hasta el máximo
        I5 = max(map(max, I4)) - I4
        #Normalizamos
        I5 = I5/max(map(max, I5))
        #Realizamos el intensity weighting
        I6 = I5*I3
        #Normalizamos de nuevo
        I7 = I6/max(map(max, I6))
        x3 = I3
        I3 = I7
    I3[np.isnan(I3)] = 0
    IMSSR = I3*img

    return IMSSR

Como primer experimento parece interesante ver si la diferencia de no usar esta ponderación en la cuenta tiene algún efecto apreciable por el ojo humano. Para esto se procede a mostrar las imágenes obtenidas con los parámetros Aplicación=5 , hs=3 , Orden = 1 y un procesamiento temporal de media.

Figura 8: Comparación MSSR con y sin Kernel Espacial

Más allá de las comparaciones que podemos hacer con nuestra vista parece relevante ver qué diferencia objetiva hay entre ambas imágenes. Para esto tomamos la diferencia media entre ambas imagenes, la diferencia máxima y la diferencia acumulada

Tipo de diferencia	Valor(px)
Diferencia media	0.1315602703735406
Diferencia máxima	11.33741501570907
Diferencia acumulada	2397.685927557777

Una vez determinada que no hay mucha diferencia entre las imágenes procedimos a ejecutar 1000 veces ambos algoritmos en la misma imagen con los mismos parámetros. Encontramos que hay una diferencia en el tiempo de corrida promedio de 0.0011773517131805425 segundos lo que se traduce a una mejora del 5,6% en los tiempos de corrida.